Introduction

The AO-2 adaptive optics system improves your telescope's resolution over a wide variety of conditions. In fact, it usually more than doubles the photographic resolution. This note explains these assertions, and shows how this is done. The arguments here are mostly theoretical, since everyone's telescope and observing site is a little bit different. The world's largest observatories are incorporating adaptive optics image stabilization into their telescopes, and their reasons are based on the same kind of analysis presented here. High resolution is obtained not by going to larger telescopes, but by using adaptive optics. The notes here refer to image motion due only to the atmospheric image motion - the telescope vibrations and clock drive errors are already assumed to be completely eliminated!

The seeing diameter is the key parameter in atmospheric turbulence

Planet motion due solely to atmospheric turbulence has been recognized for many years as a source of image blur. For professional observatories, where the telescopes and clock drives are nearly perfect, the first problem in high resolution is image motion. The amount of image motion can be calculated, and depends primarily on the "seeing diameter". At the worlds best observatory sites, the average seeing diameter in the visible part of the spectrum is 13 cm. When the seeing is great, this diameter may increase to 25 cm or rarely, to as large as 35 cm. In more typical sites, the seeing diameter may only be 5 cm. Clearly, the range of seeing varies quite a bit. Charts or graphs of telescope performance often use the ratio of the telescope diameter over the seeing diameter. Typically, ratios less than about 3 are required for high resolution performance.

There are ways to accurately measure the seeing diameter, but a few rules of thumb give a good idea of how large the seeing diameter is at your observatory. Observe a perfectly focused star, and try to estimate its diameter due to image motion. (Don't confuse clock drive error with atmospheric turbulence). A reticle eyepiece at high magnification may be helpful. If the Airy disk is visible and practically stationary, the seeing diameter is roughly equal or larger than your telescope aperture. If the Airy disc is distinct, but the total image wander is about 1 arcsecond, then the seeing diameter is about 10 cm. If the total image wander is about 2 arcseconds, the seeing diameter is about 5 cm. If the Airy disk is not visible, then the seeing diameter is less than about 5 cm. In my backyard, observing with an 20 cm SCT, the seeing diameter is often only 5 cm to 8 cm, and is only occasionally as large as 10 cm.

An image, whether on film or from a CCD, will record this image motion as a blur if the exposure is longer than about 0.1 second. For any type of high resolution photographs, the exposures will be longer than this. If you use film, the long effective focal ratio of the eyepiece projection system, combined with fine grain slides or negatives, results in exposures many seconds long. If you use a CCD camera with two pixels per Airy disk and an IR blocking filter, exposures of at least ½ second are required to use the full dynamic range of the CCD, even for Mars. If colored filters are used to reduce atmospheric dispersion and to produce color images, the exposures are again well over 1 second long. This means that image motion must be reduced for high resolution photography!

Image motion stabilization reduces the recorded image blur

The improvement in the resolution can be calculated once the seeing diameter is known, and the improvement is pretty much the same over a broad range of conditions. Here, I use the diameter of the Airy disk at half its maximum intensity to define the resolution. This is the standard definition of resolution for smooth images. Since I am comparing improvement ratios, the exact definition isn't that important.

During great seeing conditions with a 20 cm telescope, the seeing diameter is 10 cm, and the telescope diameter/seeing diameter = 2. By using the AO-2 adaptive optics image stabilizer, the resolution improvement ratio is 1.9. This means features 1.9 times smaller than before stabilization will be resolved! Under average seeing, the improvement grows to 2.1 times better. For other telescopes and other seeing conditions, the graph shown here gives the resolution improvement. Note that for amateur telescopes from about 15 cm to 50 cm, the improvement is always greater than 1.5, and is often greater than 2. The region of most improvement for 20 cm to 40 cm telescopes is when the seeing diameter is around 10 cm. This represents good seeing, when high resolution detail is visually obvious. For poor seeing, the improvement ratio drops to 1.5, but the seeing is so bad here in the first place that even reducing this motion will not likely result in high resolution images. The drop in improvement for large seeing diameters is compensated by the lower initial image motion, so less image stabilization is required. Photography approaching the diffraction limit is thus possible not only when the seeing is perfect, but also during just "good" seeing, when using the AO-2 adaptive optics image stabilization!

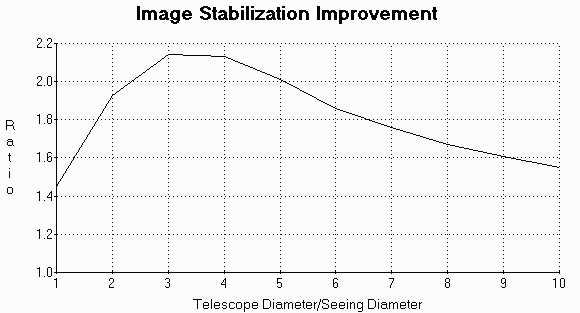
How do these numbers compare with actual results? Professional observatories have been concerned with this problem for years, and they have measured their improvement with image stabilizers, using real stars. They get results that follow this curve!

Depending on how you measure resolution, detailed computer simulations can give even better results. One astronomer's detailed computer simulation shows that the improvement near the top of the curve is not 2.1 times, but 3.7 times better. The above curve depends on how you measure resolution, and may be a conservative estimate when all factors are considered.

Remember that this improvement ratio is calculated for perfect telescopes and perfect clock drives. Even professional observatories have clock drive errors on the order of 0.1 arcsecond per second! Semi-professional clock drives may have tolerances of ±5 arcseconds. Commercial clock drives on SCT telescopes have typical drive errors of 0.5 arcsecond per second, cumulative to 50 arcseconds over a few minutes. Attempting to record sub-arcsecond planetary images is simply not possible unless this image motion is corrected! Considering both atmospheric turbulence and clock drive errors, the photographic resolution will be more than doubled using the AO-2 adaptive optics image stabilization.

The MTF curve describes contrast improvement in a more general way

For a more detailed analysis, optics designers use a tool called the MTF curve. A good explanation of this curve appeared in the July 1993 issue of Sky & Telescope, where it was used to explain the effect of the secondary mirror obstruction in telescopes. The same type of curve can be used to analyze the effect of image motion. One advantage to using these curves is that the contrast improvement for different targets can be determined. Although the technique is very powerful, it is also somewhat complicated, so we will simplify the analysis here as much as possible.

The chart shown here is for an object with an intrinsic contrast of 20%, for a 20 cm telescope during average (7 cm) seeing. The same curves can be scaled for different apertures, as long as the telescope diameter/seeing diameter is the same (2.9). The curves change for different ratios, but the same general conclusions can be drawn as explained here.

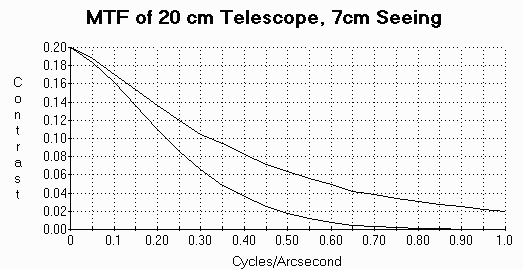
The two curves represent the image contrast resulting from an uncorrected telescope (the lower curve) and the image stabilized telescope (highest curve). The maximum contrast was limited to 20% to simulate the observation of planetary images, just like the Sky & Telescope article. The perfect telescope, without the atmosphere, is higher than both curves, and is not shown. These curves are for stationary CCD or photographic imaging; the eye can follow some motion, so the curves don't represent that kind of detector - more about that later.

The contrast can be analyzed in two directions, representing the limiting resolution and the contrast improvement. We will discuss both approaches, starting with the limiting resolution.

The MTF curves show the tremendous improvement that image stabilization provides at high resolutions. For example, at 2% contrast (0.02 on the vertical scale), the limiting resolution doubles from about 0.5 cycles/arcsecond (2 arcseconds resolution) on the uncorrected curve to 1.0 cycle/arcsecond (1 arcsecond resolution) on the image stabilized curve. This is still low compared to the diffraction limit of a perfect telescope, where the 2% contrast is at 1.56 cycles/arcsecond (0.64 arcsecond resolution), reflecting the fact that good seeing is still required to get diffraction-limited photos. During better seeing, both curves are higher, especially at higher resolution. The curve representing the stabilized telescope will always cross a given contrast level at a higher resolution, especially at low contrast.

Alternatively, the contrast improvement can be determined from the graphs by reading vertically. At 0.4 cycles/arcsecond (2.5 arcsecond resolution), the contrast resulting from image stabilization improves from about 3.5% to about 8%, more than doubling the contrast. At higher resolutions, the improvement ratio grows even larger. Where the unstabilized telescope cannot possibly resolve 1 arcsecond images, the stabilized image has a 2% contrast, easily detectable by CCD image processing.

The lower effective MTF due to image motion cannot be compensated by using a larger telescope. For some types of aberration, getting a higher MTF is accomplished simply by using a larger aperture. This effectively stretches the lower curve to the same position as the stabilized curve. For atmospheric image motion, however, going to a larger aperture has practically no effect on the lower curve. This is because the curve degrades not because of diffraction or other telescope defects, but is due to the effective atmospheric seeing diameter. Going to a larger telescope will not improve the resolution. The only way to increase the contrast shown at the right side of the curve, or to increase the resolution at a given contrast, is to stabilize the motion.

The AO-2 is not a perfect stabilizer, working better at low frequencies than high frequencies. This still gives nearly ideal performance, however, because most of the image motion is at low frequencies. The MTF curves show that photographic performance is more than doubled at high resolution, no matter which kind of resolution measurement is used. This holds true over a wide variety of telescope and seeing conditions.

Visual resolution improvement results from reduction in high frequency motion

For visual resolution improvement, more analysis is necessary. Because the eye follows slow motions, the resolution improvement is not as great. One way to study this situation is in terms of the effective diameter due to image motion. The following analysis is only for atmospheric turbulence, assuming absolutely no wind or other telescope vibration. If these are included, the AO-2 will help even more than the theoretical minimum described here.

For typical planet brightness levels, the eye can follow motions up to about 10 oscillations per second (10 Hz). Motions faster than this result in a blurred image, reducing contrast and resolution. Image stabilization improves resolution by reducing the high frequencies as well as the low frequencies. The problem here is to determine how much motion occurs at low frequencies and how much motion occurs at high frequencies.

A typical case is analyzed here; again, every observatory site and every telescope may be a bit different, but the same general conclusions can be drawn. I again choose the 20 cm telescope and 7 cm seeing as the representative case.

Typical atmospheric turbulence image motion, just including motions faster than 10 Hz, is 0.84 arcseconds, compared to the Airy disk of 0.57 arcseconds. These diameters add like the sides of a right triangle, so the resulting blurred diameter is 1.02 arcseconds, 1.8 times the diffraction limit. When the AO-2 is used to stabilize the image, slow motions are reduced more than faster motions, so calculations must be based on the actual frequency response of the AO-2. Doing this for any of the brighter planets, the left-over image motion at high frequencies (greater than 10 Hz) gives 0.5 arcseconds. This results in an apparent visual diameter of 0.75 arcseconds, only 30% over the diffraction limit! This visual improvement ratio is 1.35 times the uncorrected telescope. This is not as good as the photographic improvement ratio, but it is like converting a 20 cm telescope to a 27 cm telescope. For assessing very fine detail, this is still substantial improvement.

Similar results are found for different telescopes under different seeing conditions. If the seeing is poor, however, then higher-order aberrations will blur the image too much. Basically, if the Airy disk is visible to the eye, then for telescopes between 15 and 30 cm, the visual improvement will be at least 20%. If the seeing is excellent, or a 40 cm telescope is used, the AO-2 improvement will also be reduced; typical atmospheric turbulence improvements may only be 5-10%. Photographically, however, the improvement will still be doubled, as explained earlier.

Conclusions

All of the above analyses applies strictly to atmospheric turbulence induced motion. For other sources of image motion, such as wind, ground, focus, or clock drive vibration, or clock drive gear error or polar alignment error, the AO-2 is even more effective. Visually, these other rapid motions are sometimes large enough that they can be even more disruptive than atmospheric motion.

While these notes have been pretty technical, the final proof is in the photos. They show the improvements due to atmospheric turbulence, telescope vibrations, and clock drive errors. Some were taken in average seeing, some in better seeing. In every case, the improvement in resolution has been significant, limited only by the telescope optics and smaller atmospheric errors. Adaptive optics image stabilization is the key to high resolution astronomy!

All text and images are owned by Stellar Products, 1992-2003. Any use by others without permission of Stellar Products is prohibited.

Links to other Stellar Products pages: